AC自动机 | 多字符串匹配你会吗？

字符串匹配算法应该每个学过编程的同学都会，KMP算法曾是我的噩梦（好像现在也不记得了-_-）。不过传统的字符串匹配算法都是匹配一个子串，我们今天说的这个是如何同时匹配多个子串，而且时间复杂度平均为线性的，它叫AC自动机。

问题描述

给定一个待搜索m长度的字符串s，以及一个包含n个词（或者说子串）的词典，要求能够找出s中包含的所有在词典中的子串。

应用场景

需求才是让你能够深入研究算法的最大动力，所以我们要知道学习每一个算法可以用在什么地方（我是实用主义者）。

我这边的场景是我们有一个专业领域的词表了（可以认为是一些实体的名称，但是我们没有NER模型），想要在大语料上找到含有这些词汇的句子或者段落，所以只能强行按照字符串匹配的算法来找到这些文本。还有的场景就是搜索引擎里面对query进行匹配，尽可能多的找出里面的可能的关键词，然后提高召回。

如果是最简单的想法可能就是一个for循环遍历词表，判断在不在文本里面。词表小的时候其实还好，但是如果词表大了，那么这个效率是很低的。

思想

看了很多资料都说了解AC自动机得先了解KMP算法，导致我先去看了学习了KMP。但是从我看下来，要学习AC自动机根本没必要先看KMP。

我说说我自己对AC自动机的理解：

• 首先就是要构建一个字典的trie树，一方面是方便查找，一方面也是要存一些信息进行模式匹配
• 在trie树上构建失配指针，使这个trie树成为AC自动机
• 然后就是在自动机上进行字符串匹配了

如果你不了解trie树的话，可以先百度一下再回来。

失配(fail)指针

为什么要构建失配指针？

假设我们的字典包含这些词{a,ab,bab,bc,bca,c,caa}，待匹配的字符串是abccab。构建的trie如下所示：

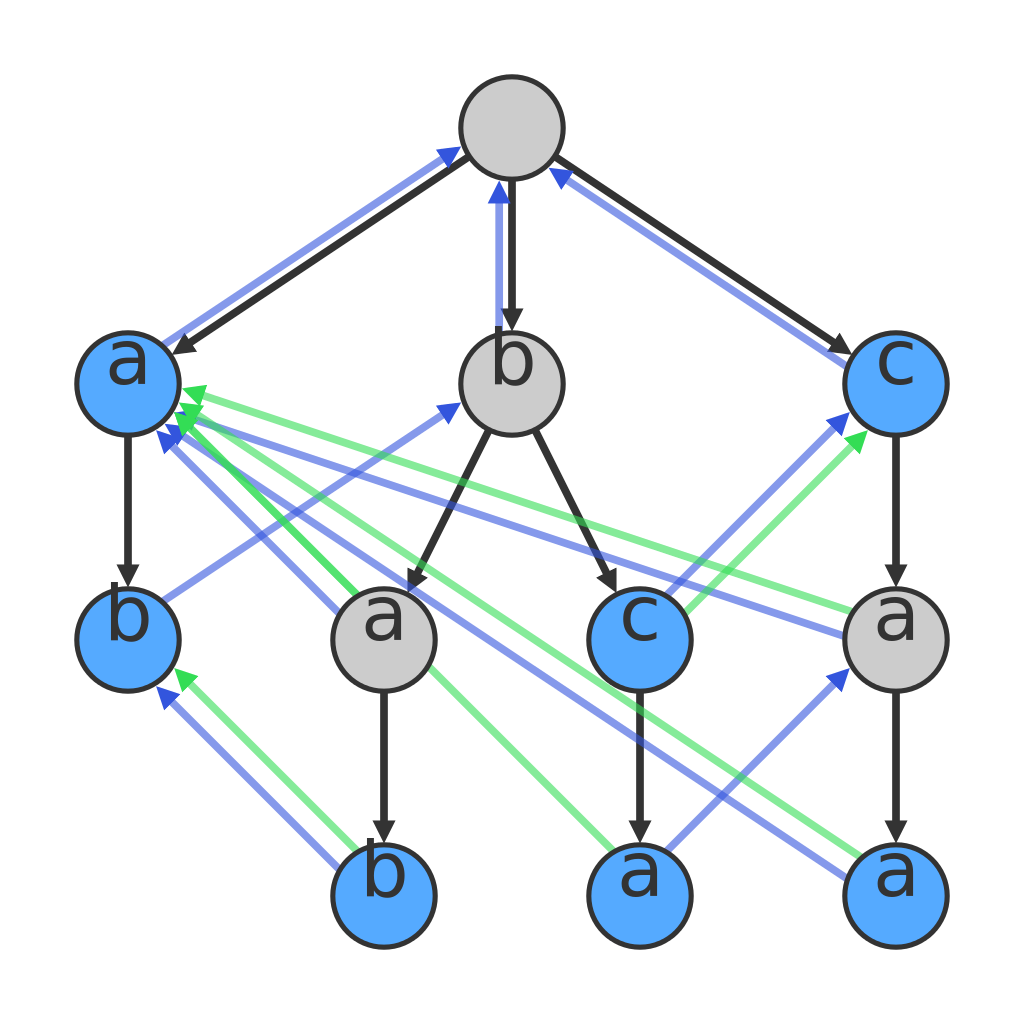
目前我们只关心黑色的箭头，因为这个代表普通的trie树结构。现在开始从字符串i=0的字符开始匹配，trie从root节点开始a,ab你可以匹配到，但是到c的时候你发现匹配失败了，这时候正常的话你需要将i+=1从下一个字符开始匹配，trie又开始从root匹配。但是这里的问题是，我们已经匹配过ab了，说明下一个字符肯定是b，我们完全没有必要再从trie的root开始匹配，这时候我们从root下面的b节点开始匹配就好了，也就是失配指针（图中蓝色的箭头）指向的地方。

其实这里我们就发现了，失配指针其实存储了字典中词的一些信息，避免我们每次从头开始匹配，从这里看的话其实跟KMP还是有共性的，存储子串中的一些信息。

如何构造失配指针

进一步的话，其实失配指针代表的是子串之间后缀和前缀之间的关系。对于字符串bca，它的严格后缀（我理解是不包括自己的后缀）是ca,a,None，前缀是bca,bc,b,None；对于另外一个字符串caa，它的前缀是caa,ca,c,None，我们发现bca的后缀其实出现在caa的前缀中，因此bca在匹配下一个字符失败的时候，我们可以跳到caa的第一个a节点上继续匹配下一个字符，因为ca已经匹配过了。

节点i失配指针指向的节点j代表的意思是到节点i为止的字符串最长的严格后缀等于到节点j为止的字符串，对于上面的bca的例子，如果trie树中存在ca字符串，那么失配节点指向的就是ca的a节点；如果trie树中只有a，那么就是a节点了；如果都不存在，那么就是root节点，我们要从头开始匹配。

注意这里提到的是最长的严格后缀，大家可以想想为什么一定要最长？因为我们匹配的时候是从左到右一个一个字符匹配的，如果不是最长的话我们就丢失了匹配的信息了，举例来说有bcacay字符串待匹配，有子串bcacax,cacay，如果不是最长的话bcaca就可能会指向cacay的第一个ca了，那么就丢掉了匹配到的caca信息，造成匹配失败。

关于如何构造失配指针，其实是一个BFS的算法，按照层序遍历的方法构建：

• 首先root节点不管，root节点的孩子肯定都是指向root节点的，因为他们的后缀都是空。
• 假设我们已经有了节点x的失配指针，那么我们如何构造他们孩子child的失配指针呢？因为失配指针保证的是最大后缀，因此他肯定保证了x之前的字符都是匹配的。我们知道x的失配指针指向的是节点x的最大后缀y，因此我们只要看看节点y的孩子节点中是不是有child节点对应的字符，如果有的话那很好，child的失配指针就是y的那个孩子；
• 那如果没有呢，那我们就继续看y节点的失配指针了，因为他也指向y节点的最大后缀，也保证了跟x字符是匹配的。这样一直下去直到相应的节点，或者直到根节点。

这个最关键的就是构建失配指针。为什么要构建失配指针？

大家可以参考上面那张图，脑中YY一下{a,ab,bab,bc,bca,c,caa}的构建过程是不是这样。

查找

然后说说查找的过程。其实已经有了AC自动机，查找就是很自然的事情了。

从左到右去匹配字符串，如果能够匹配到trie树的节点就继续匹配，如果匹配不到的话呢就去看看节点的fail节点，因为这保证的是你之前匹配到的字符都是相同的。然后对于每个节点，都去查找一下是否有输出，没有输出就看看fail节点有没有输出，直到root节点。这样就把每个节点的匹配字符串都输出来了。

有同学可能发现图中有绿色的箭头，其实指向的是通过fail节点能够到达的最近的有效子串，这样避免我们递归去找子串了。

实现

先定义节点:

class Node(object):
    def __init__(self, value='', finished = False):
        self.children = {}
        self.value = value
        self.fail = None
        self.key = ''
        self.finished = finished
        
    def child(self,value):
        '''get the child based on the value
        '''
        return self.children.get(value,None)

首先构建字典树，就是传统的trie树的构造，我这里肯定很多没有优化了，后面可以介绍一下双数组trie树，比较适合中文的trie数构建。

def build_trie(root, key_words):
    def add_word(root, word):
        for c in word:
            child = root.child(c)
            if not child:
                child = Node(value=c)
                root.children[c] = (child)
            root = child
        root.key = word
        root.finished = True
            
    for word in key_words:
        add_word(root,word)
    return root

下面就是构造AC自动机了，采用BFS的方法，用父节点的fail来更新子节点的fail。

from collections import deque

def build_ac(root):
    q = deque()
    q.append(root)
    while q:
        node = q.popleft()
        for value,child in node.children.items():
            if node == root:
                child.fail = root
            else:
                fail_node = node.fail
                c = fail_node.child(value)
                if c:
                    child.fail = c
                else:
                    child.fail = root
            q.append(child)
    return root

最后是查找的过程，从左到右查询query，如果匹配的话就看看node节点之前有没有可以输出的节点，如果不匹配的话就找fail节点。

def search(s, root):
    node = root
    for i,c in enumerate(s):
        while node and not node.child(c):
            node = node.fail
        if not node:
            node = root
            continue
        node = node.child(c)
        out = node
        while out:
            if out.finished:
                print(i,out.key)
            out = out.fail

我这里没有实现绿色的指针，所以输出的时候还是要递归一下，有兴趣的同学可以自己实现一下。

简单的测试：

key_words = 'a,ab,bab,bc,bca,c,caa'.split(',')
trie = Node()
build_trie(trie,key_words)
build_ac(trie)
search("abccab",trie)
# 输出应该为：
# 0 a
# 1 ab
# 2 bc
# 2 c
# 3 c
# 4 a
# 5 ab

推荐个已经实现好的python库pyahocorasick，我们在用这个。